I.6. Coeficienți calorici.

• I.6.1. Căldura specifică.
• I.6.2. Capacitatea calorică.

Experiment

12. De cine depinde căldura absorbită de un corp ?

Materiale necesare: două pahare Berzelius, apă rece de la robinet, spirtieră, sită de azbest, trepied, termometru, cronometru, ulei.

A) Care masă de apă absoarbe mai multă căldură, 50 g sau 100 g?

Descrierea experimentului:

• Pune într-un pahar 50 g de apă și introdu în apă un termometru. Încălzește la flacăra unei spirtiere, apa prin intermediul sitei de azbest de pe trepied.

Atenție

Acest experiment se efectuează numai în prezența unui adult!

Când lucrezi cu surse de foc ai grijă să ai părul strâns și să nu porți haine cu mâneci largi! Atenție când lucrezi cu apă caldă să nu te arzi!

• Cronometrează timpul în care masa de 50 g apă și-a mărit temperatura cu 10 °C: t₁ = 39 s.

• Pune într-un pahar o masă de 100 g de apă și introdu în apă un termometru. Încălzește apa la flacăra unei spirtiere, prin intermediul sitei de azbest de pe trepied.

• Cronometrează timpul în care masa de 100 g apă și-a mărit temperatura cu 10 °C: t₂ = 48,6 s.

• Depinde căldura absorbită de masa corpului ?

Cu cât timpul de încălzire este mai mare, cu atât și căldura absorbită este mai mare.

Observaţie

O masă de 100 g apă absoarbe mai multă căldură decât o masă de 50 g apă.

Concluzia experimentului:

• Căldura primită/cedată de un corp în procesul de încălzire/răcire este direct proporțională cu masa corpului: Q ~ m.

B) Depinde căldura absorbită de variația temperaturii?

Descrierea experimentului:

• Cronometrează timpul în care o masă de 100 g apă și-a mărit temperatura cu 20 °C: t₃ = 2 min 3 s. Compară cu timpul în care aceeași masă de 100 g apă și-a mărit temperatura cu 10 °C.

• Depinde căldura absorbită de variația temperaturii corpului ?

Observaţie

O masă de 100 g apă absoarbe mai multă căldură pentru a-și mări temperatura cu 20 °C, decât o masă de 100 g apă pentru a-și mări temperatura cu 10 °C.

Concluzia experimentului:

• Căldura primită/cedată de un corp în procesul de încălzire/răcire este direct proporțională cu variația temperaturii corpului: Q ~ ΔT.

C) Depinde căldura absorbită de substanța corpului?

Descrierea experimentului:

• Pune o masă de 100 g ulei într-un pahar Berzelius și introdu termometrul în ulei.

• Măsoară temperatura inițială a uleiului care trebuie să fie aceeași cu cea a apei (30 °C).

• Cronometrează timpul în care uleiul și-a mărit temperatura cu 20 °C: t₄ = 46,55 s. Compară cu timpul în care o masă de 100 g apă și-a mărit temperatura cu 20 °C.

• Depinde căldura absorbită de substanța din care este alcătuită corpul ?

Observaţie

O masă de 100 g apă absoarbe mai multă căldură decât o masă de 100 g ulei, pentru a-și mări temperatura cu 20 °C.

Concluzia experimentului:

• Căldura primită/cedată de un corp în procesul de încălzire/răcire depinde de natura substanței. Deci se poate defini o constantă de material numită căldură specifică, notată cu c.

Deci căldura primită/cedată de un corp la încălzire/răcire depinde direct proporțional de trei factori: masa corpului, variația temperaturii și natura substanței corpului.

Definiţie

Coeficienții calorici reprezintă mărimile fizice care caracterizează schimbul de căldură dintre sistemele termodinamice.

Printre cei mai importanți avem:

• Căldura specifică (c);
• Capacitatea calorică (C).

I.6.1. Căldura specifică.

Definiţie

Căldura specifică(c) reprezintă mărimea fizică ce caracterizează căldura absorbită/cedată de 1kg de substanță pentru a-și mări/micșora temperatura cu un grad.

Căldura specifică este o constantă de material și o găsim în tabelul cu constante de la sfârșitul acestui capitol.

important

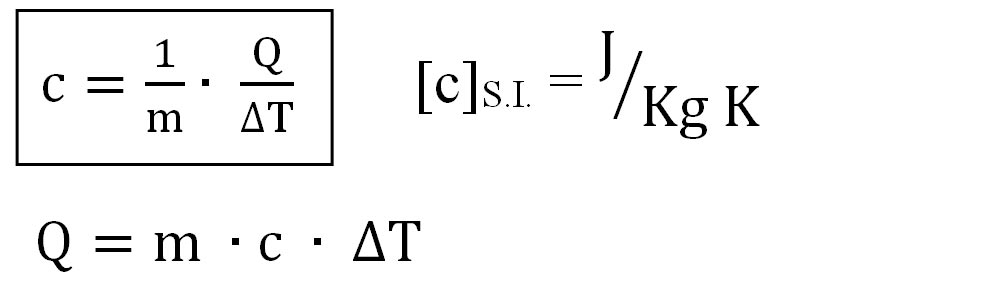
Căldura primită/ cedată de un corp(Q) în procesul de încălzire/ răcire are următoarea formulă:

m = masa corpului

c = căldura specifică (constantă de material, specifică fiecărei substanțe)

ΔT = T_finală - T_inițială, variația temperaturii corpului (adică, cu cât crește/ scade temperatura lui)

Q_primită > 0

Q_cedată < 0

La ecuația calorimetrică vom scrie Q_primită= | Q_cedată |

Observaţie

Căldurile specifice pot avea valori diferite pentru aceeași substanță dacă aceasta se găsește în stări de agregare diferite.

c_apă ≠ c_gheaţă

Atenție

Acest experiment se efectuează numai în prezența unui adult!

Când lucrezi cu surse de foc ai grijă să ai părul strâns și să nu porți haine cu mâneci largi! Atenție când lucrezi cu apă caldă să nu te arzi!

I.6.2. Capacitatea calorică.

Definiţie

Capacitatea calorică (C) – reprezintă mărimea fizică ce caracterizează cantitatea de căldură necesară sistemului termodinamic pentru a-și varia temperatura cu un grad.

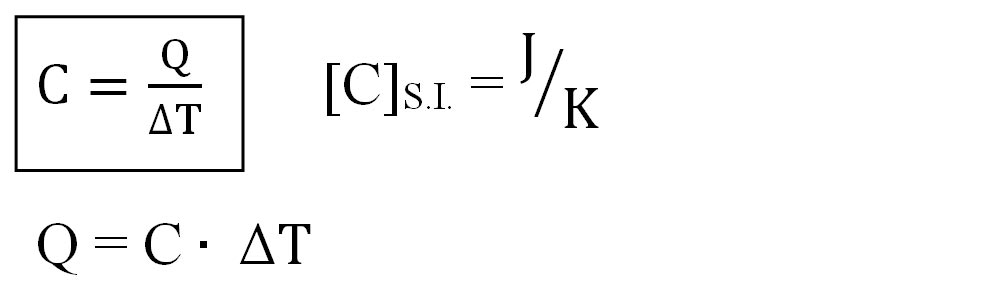
Observaţie

Sistemul termodinamic poate reprezenta un calorimetru sau un vas, în care schimbul de căldură este permis doar între corpurile introduse. Capacitatea calorică a unui calorimetru este înscrisă pe vasul respectiv la fabricația acestuia.

Experiment

13. Calcularea căldurii specifice a unui corp solid

Materiale necesare: apă rece de la robinet, sită de azbest, stativ, trepied, termometru, calorimetru (vas care izolează termic corpurile din interiorul său de cele din exterior), cilindru de cupru, pahar Berzelius, spirtieră, cârlig.

Atenție

Acest experiment se efectuează numai în prezența unui adult!

Când lucrezi cu surse de foc ai grijă să ai părul strâns și să nu porți haine cu mâneci largi! Atenție când lucrezi cu apă caldă să nu te arzi!

Descrierea experimentului:

• Măsoară cu cântarul masa apei: m₁ = 100 g = 0,1 kg.
• Măsoară cu termometrul temperatura apei: t₁ = 30 °C .
• Măsoară cu cântarul masa cilindrului de cupru: m₂ = 78 g = 0,078 kg
• Încălzește apă într-un pahar Berzelius cu ajutorul spirtierei și a trepiedului cu sită.
• În apa caldă pune cilindrul de cupru și termometrul. Lasă-le câteva minute și apoi citește temperatura cilindrului de cupru încălzit: t₂ = 90 °C.
• Pune în calorimetru apa rece cântărită.
• Cu cârligul metalic ia corpul din pahar și pune-l rapid în apa din calorimetru.
• Acoperă calorimetrul și agită ușor apa din el.
• Urmărește indicațiile termometrului până când temperatura nu se mai modifică. Aceasta este temperatura de echilibru, notată cu t_e = 35 °C, care reprezintă temperatura finală pentru toate corpurile aflate în contact termic.

Observaţie

Apa rece va primi căldură, iar cilindrul de cupru este corpul cald, care cedează căldură.

• Neglijăm capacitatea calorică a calorimetrului, pentru simplificarea calculelor.

• Δt₁ = t_e – t₁ = variația (creșterea) temperaturii apei (temperatura finală minus cea inițială).

• Δt₂ = t_e - t₂ = variația (scăderea) temperaturii cilindrului (temperatura finală minus cea inițială).

• Scriem ecuația calorimetrică : | Q_cedată | = Q_primită

  • | Q_cedată | = m₂ ∙ c₂ ∙ Δt₂ = m₂ ∙ c₂ ∙ (t_e - t₂)

  • Q_primită = m₁ ∙ c₁ ∙ Δt₁ = m₁ ∙ c₁ ∙ (t_e – t₁)

  • | m₂ ∙ c₂ ∙ (t_e - t₂) | = m₁ ∙ c₁ ∙ (t_e – t₁)

• Obţinem formula pentru determinarea căldurii specifice a cuprului:

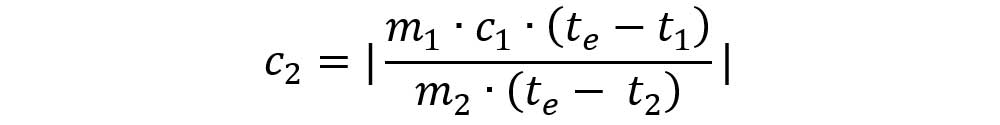
• Înlocuim în formulă valorile din experimentul nostru:

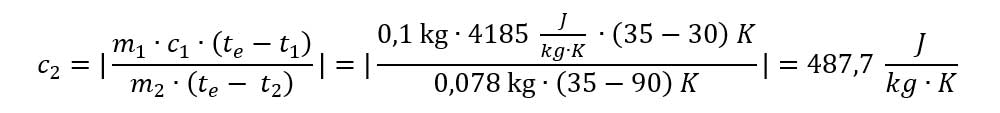
Concluzia experimentului:

Comparăm cu căldura specifică a cuprului din tabel (385 J/kg∙K) și observăm că valoarea experimentală este destul de departe de valoarea reală. Ca surse de erori am descoperit: citiri neatente ale temperaturilor corpurilor, a durat cam mult timp până am închis capacul calorimetrului, am realizat o singură determinare în loc de 3 determinări, nu am luat în calcul și capacitatea calorimetrului.

Observaţie

În cazul sistemelor neomogene de corpuri, ca în cazul acestui experiment, este necesar să cunoaștem temperaturile inițiale ale corpurilor din sistem, masele lor și căldurile lor specifice. Astfel vom putea ști evoluția termică a acestui sistem de corpuri.

Problemă rezolvată

1. Într-o masă de 20 g de glicerină se pune o masă de 50 g fier la temperatura de 90 °C. Știind că temperatura de echilibru este de 50 °C, află temperatura inițială a glicerinei.

Se dă:

• căldura specifică a glicerinei de 2400 J/Kg∙K
• căldura specifică a fierului de 450 J/Kg∙K

Rezolvare

• Înainte de a scrie datele problemei, se stabilește corpul rece, respectiv cel cald:

  • Corp 1: glicerină : rece =˃ primește căldură: Q_primită

  • Corp 2: fier : cald =˃ cedează căldură: Q_cedată

• Scriem datele problemei, punând indice 1 la datele despre glicerină și indice 2 la datele despre fier. Transformăm mărimile din date în SI, cu excepția temperaturii, deoarece diferența dintre două temperaturi în grade Celsius este egală cu diferența temperaturilor în Kelvin.

  • m₁ = 20g = 0,02 kg

  • c₁ = 2400 J/kg∙K

  • m₂ = 50 g = 0,05 kg

  • t₂ = 90 °C

  • c₂ = 450 J/kg∙K

  • t_e = 50 °C

  • t₁ = ?

• Calculăm căldura cedată:

  • Q_cedată = m₂ ∙ c₂ ∙ Δt₂ = 0,05 kg ∙ 450 J/kg∙K ∙ (t_e - t₂) K = 0,05 ∙ 450 ∙ (50 – 90) J = -900 J

• Calculăm căldura primită:

  • Q_primită = m₁ ∙ c₁ ∙ Δt₁ = 0,02 kg ∙ 2400 J/kg∙K ∙ (t_e – t₁) K = 2 ∙ 24 ∙ (50 - t₁) J

• Scriem ecuația calorimetrică : | Q_cedată | = Q_primită

  • | m₂ ∙ c₂ ∙ (t_e – t₂) | = m₁ ∙ c₁ ∙ (t_e – t₁)

• Facem calculele matematice:

  • 900 J = 48 ∙ 50 - 48 ∙ t₁ J
  • 48 ∙ t₁ = 2400 - 900
  • 48 ∙ t₁ = 1500
  • t₁ = 31,25 °C

Problemă rezolvată

2. Într-un calorimetru a cărui capacitate calorică este 80 J/kg, se pune o masă de 200 g apă la temperatura de 10 °C. În apa din calorimetru se introduce un corp de aluminiu care cântărește 100 g, cu temperatura de 100 °C. Care este temperatura finală a celor două corpuri ? Se dă: căldura specifică a apei de 4185 J/kg∙K și căldura specifică a aluminiului de 880 J/kg∙K. Capacitatea calorică a calorimetrului este C = 80 J/kg.

Rezolvare

• Înainte de a scrie datele problemei, se stabilește corpul rece, respectiv cel cald:

  • Corp 1: apa și calorimetrul : rece =˃ primește căldură: Q_primită

  • Corp 2: aluminiul : cald =˃ cedează căldură: Q_cedată

• Scriem datele problemei, punând indice 1 la datele despre apă și indice 2, la datele despre aluminiu. Transformăm mărimile din date în SI, cu excepția temperaturii, deoarece diferența dintre două temperaturi în grade Celsius este egală cu diferența temperaturilor în Kelvin.

  • C = 80 J/K

  • m₁ = 200 g = 0,2 kg

  • t₁ = 10 °C

  • c₁ = 4185 J/kg∙K

  • m₂ = 100 g = 0,1 kg

  • t₂ = 100 °C

  • c₂ = 880 J/kg∙K

  • t_e = ? °C

• Calculăm căldura primită:

  • Q_primită = m₁ ∙ c₁ ∙ Δt₁ + C ∙ Δt₁ = m₁ ∙ c₁ ∙ (t_e – t₁) + C ∙ (t_e – t₁)

• Calculăm căldura cedată:

  • Q_cedată = m₂ ∙ c₂ ∙ Δt₂ = m₂ ∙ c₂ ∙ (t_e – t₂)

• Scriem ecuația calorimetrică : | Q_cedată | = Q_primită

  • | m₂ ∙ c₂ ∙ (t_e – t₂) | = m₁ ∙ c₁ ∙ (t_e – t₁) + C ∙ (t_e – t₁)

• Înlocuim datele problemei și facem calculele matematice :

  • | 0,1 kg ∙ 880 J/kg∙K ∙ (t_e - 100) K | = 0,2 kg ∙ 4185 J/kg∙K ∙ (t_e – 10) K + 80 J/K ∙ (t_e – 10) K
  • | 88 ∙ (t_e - 100) | = 837 ∙ (t_e – 10) + 80 (t_e – 10)
  • | 88 ∙ t_e - 88 ∙ 100 | = 837 ∙ t_e - 8370 + 80 ∙ t_e – 80 ∙ 10
  • | 88 ∙ t_e - 8800 | = 917 ∙ t_e – 9170

• Pentru desfacerea modulului trebuie să determinăm dacă termenul din modul este pozitiv sau negativ. Temperatura de echilibru (t_e) este întotdeauna cuprinsă între temperaturile inițiale ale celor două corpuri puse în contact termic. Ca atare, în cazul nostru 10°C < t_e < 100°C și din această cauză termenul din modul va fi întotdeauna negativ. La desfacerea modului se va schimba semnul termenului, respectiv se va înmulți cu (-1).

  • (-1) ∙ (88 ∙ t_e - 8800) = 917∙ t_e - 9170
  • -88 ∙ t_e + 8800 = 917∙ t_e - 9170
  • 17970 = 1005 ∙ t_e
  • t_e = 17970/1005 = 17,88 °C

Problemă rezolvată

3. Corpul 1 este pus în contact termic cu corpul 2.

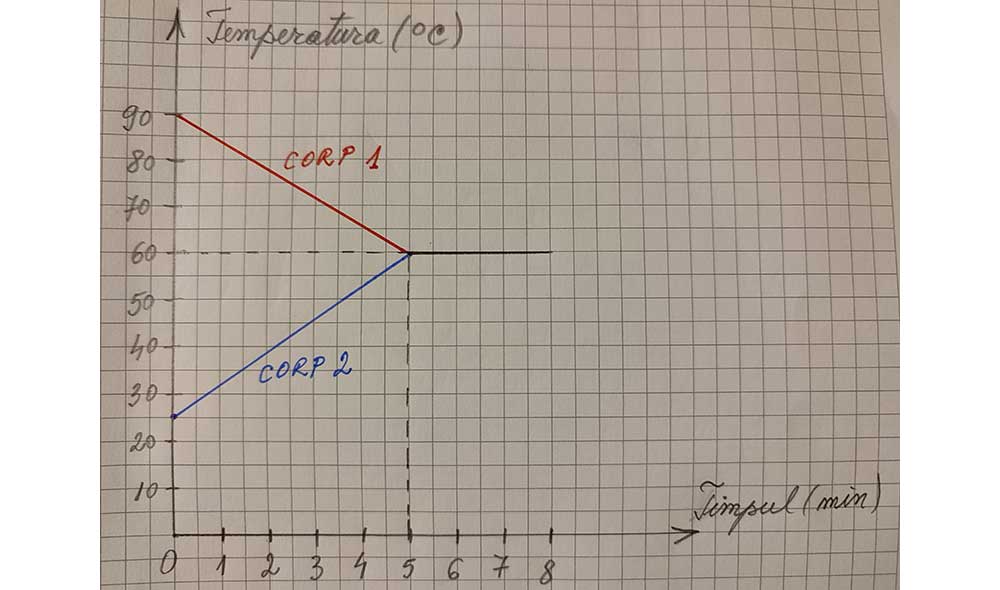
• Cât sunt temperaturile inițiale ale celor două corpuri și care este corpul rece, respectiv cald?

  • Rezolvare: t₁ = 90 °C (corpul 1 - cald) și t₂ = 25°C (corpul 2 - rece).

• Cât este temperatura de echilibru a celor două corpuri ?

  • Rezolvare: t_e = 60°C.

• După cât timp ajung corpurile la echilibru termic?

  • Rezolvare: După 5 min.