III.3. Probleme recapitulative rezolvate - Mișcare și Repaus.
🔓 Probleme recapitulative de dificultate crescută, rezolvate - Mișcare și Repaus.
1. Un mobil se mișcă uniform încetinit până la oprire cu accelerația de 1,5 m/s2, într-un minut. Ce distanță a parcurs mobilul?
Rezolvare:
Notăm datele problemei:
a = 1,5 m/s2 = constantă
v0 > 0
v = 0 (mobilul se oprește)
Δt = 1 min = 60 s
Scriem formula accelerației și calculăm viteza inițială, v0, a mobilului:
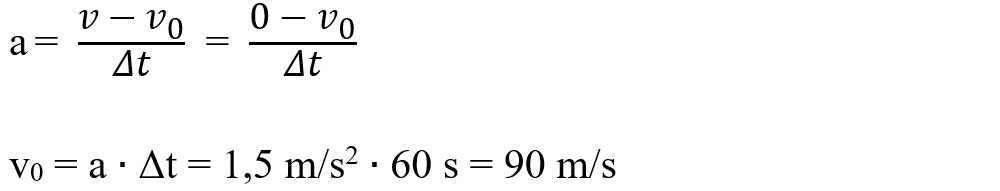
Din expresia vitezei medii obținem:

Cum în mișcarea uniform variată viteza este o funcție liniară de timp (adică crește/scade constant în aceleași interval de timp), viteza medie este media aritmetică a vitezelor inițială (v0) și finală (v), obținem:
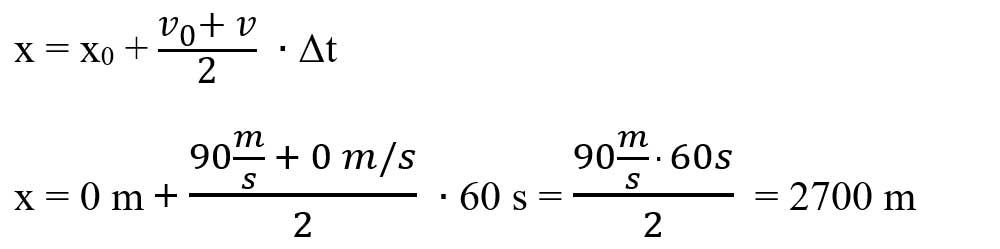
2. Determinarea legii mișcării uniform variată.
Rezolvare:
Din expresia vitezei medii obținem:

Cum în mișcarea uniform variată viteza este o funcție liniară de timp (adică crește/scade constant în aceleași interval de timp), viteza medie este media aritmetică a vitezelor inițială (v0) și finală (v), obținem:

Din formula accelerației scoatem viteza și apoi o înlocuim în formula poziției:
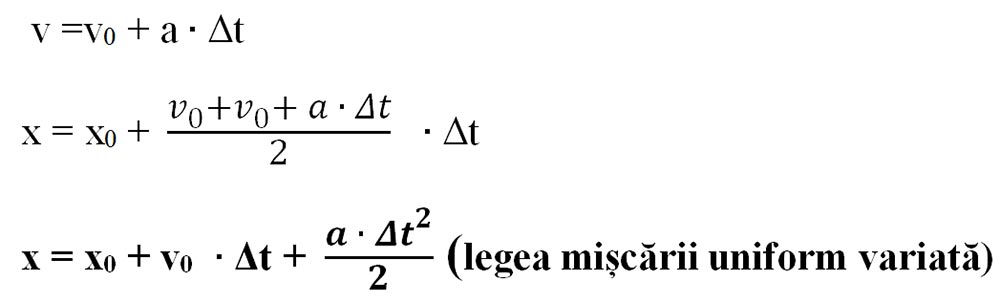
3. O mașină se deplasează cu o viteză constantă de 25 m/s. Un motociclist demarează (pornește) în momentul în care mașina a trecut pe lângă el, cu o mișcare uniform acccelerată, atingând viteza de 25 m/s în 10 s fără a înceta să accelereze. Să se determine timpul după care motociclistul ajunge din urmă mașina.
Rezolvare:
Notăm datele problemei cele referitoare la mașină cu indice 1 și cele referitoare la motociclist cu indice 2:
v1 = 25 m/s = constant
v2 = 25 m/s = crește constant în intervale de timp egale
a1 = 0 m/s2 a2 = constant
Δt2 = 10 s
Pentru cele 2 mobile avem x0, v0, t0 = 0, Δt = t
Scriem legea mișcării mobilului 1 (mașinii):

Calculăm accelerația mobilului 2 (motocicletei) și îi scriem legea mișcării:
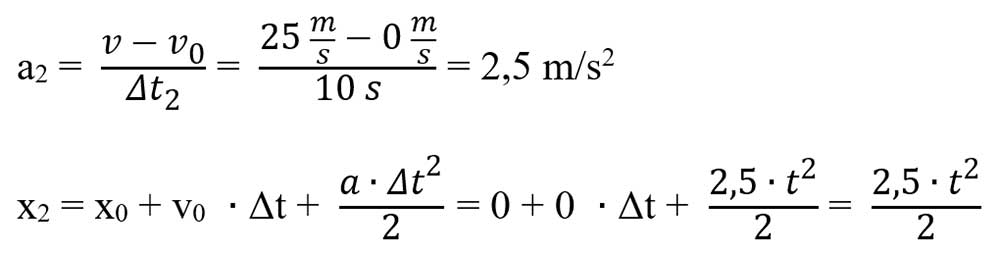
Punem condiția ca cele două mobile să se întâlnească: x1 = x2 și aflăm timpul de întâlnire:
