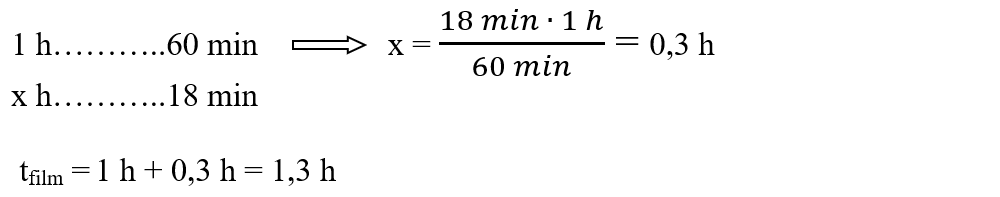Solved problems

🔓 Experimental Problem - Direct measurement of length

2.1. Determining the actual length of a body.

Required materials:
Graduated ruler, pencil.

Experiment description:

Use the graduated ruler to measure the length of the physics book.
Measure the length of the physics book several times (at least 3 times), taking care to measure correctly each time.
Fill in the following table of experimental data: you will pass your determinations and follow the steps according to the following model:

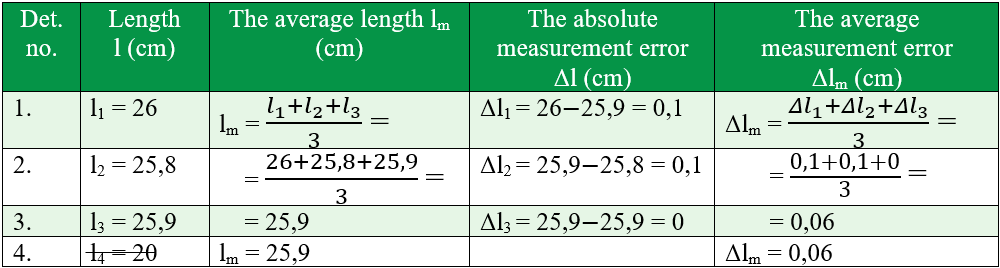
Processes experimental data.
- l is the length measured at least three times. I measured it four times, but the last value of 20 cm I excluded it, as it is far from the other values, being a rough measurement.
- l_m is the average length, ie the arithmetic average of the three measured lengths. If some values appear very different from the others, they are written in the table, but they are cut, they represent gross errors. They are not taken into account in the calculation of the average length. The arithmetic average is equal to the ratio of the sum of all lengths to the number of determinations.
- Δl is the absolute error, which is calculated by the difference between the measured length and the average length (the largest minus the smallest): Δl = l₁ – l_m sau Δl = l_m – l₁.
- Δl_m is the absolute average error, which is calculated by making the arithmetic average of the absolute errors.
After completing the table with experimental data, you must write the result of the determination, using the same number of decimals for all numbers. We will write the values with two decimal places, by rounding.

For our example: L = 25,9 cm ± 0,06 cm.

Experiment conclusion:
This result indicates that the actual value is in a range: 25,9 cm – 0,06 cm ≤ l ≤ 25,9 cm + 0,06 cm
So the real length of the physics book is: 25,84 cm ≤ l ≤ 25,96 cm.

🔓 Solved problem - Direct measurement of length

2.2. Florin wants to determine the real value of the length of the kitchen table.

Following the measurements he found the following values: 1,5 m; 1,46 m; 1,6 m ; 1,2 m; 1,56 m. How did he proceed?

Solution:

He calculated l_m = The average length, ie the arithmetic average of the four measured lengths. The value of 1.2 m is very different, it is cut and not taken into account in the calculation of the average length, being a rough measurement.

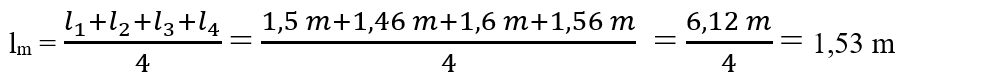
He calculated for each measurement Δl = absolute error, which is calculated by the difference between the measured length and the average length (the largest minus the smallest); Δl = l₁ – l_m sau Δl = l_m – l₁.

Δl₁ = 1,53 - 1,5 = 0,03 m
Δl₂ = 1,53 - 1,46 = 0,07 m
Δl₃ = 1,6 - 1,53 = 0,07 m
Δl₄ = 1,56 - 1,53 = 0,03 m

He calculated Δl_m = the absolute average error, which is calculated by making the arithmetic average of the four absolute errors.

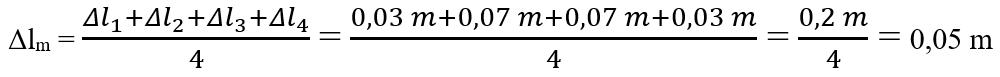
Florin wrote the result of the determination, using the same number of decimals for all numbers (values with two decimals, by rounding).
Result of the determination = The average value ± The absolute average error
l = l_average ± Δl_average = 1,53 m ± 0,05 m.

🔓 Experimental Problem - Direct area measurement

2.3. Direct measurement of the area of a leaf with graph paper

Required materials:
Graph paper, leaf, pencil.

Experiment description:

Draw on the graph paper (you can also use a math sheet that has a side of 0,5 cm and an area of 0,25 cm², but the result will not be too precise) the contour of the leaf (you can choose any shape you want, not necessarily a leaf).
Count the whole squares with an area of 1 cm² (those outlined with a blue marker), then those with an area of 0.25 cm² (those outlined in yellow), and group the whole ones and approximate them as whole squares with area of 0.25 cm². If you have patience, you can stop approximating the whole squares and count the small squares with the area of 1 mm² and their number multiplied by 1 mm² to turn it into cm², by dividing the result by 100.
To calculate the area of the leaf (S), apply the formula: S = n ∙ Su, where n = no. squares and Su = area of the chosen unit (either cm² - the largest, or 0.25 cm² - the smallest).
Draw the outline of the leaf on another graph paper and repeat the above operations so that you have at least three values of the area of the leaf of your choice.

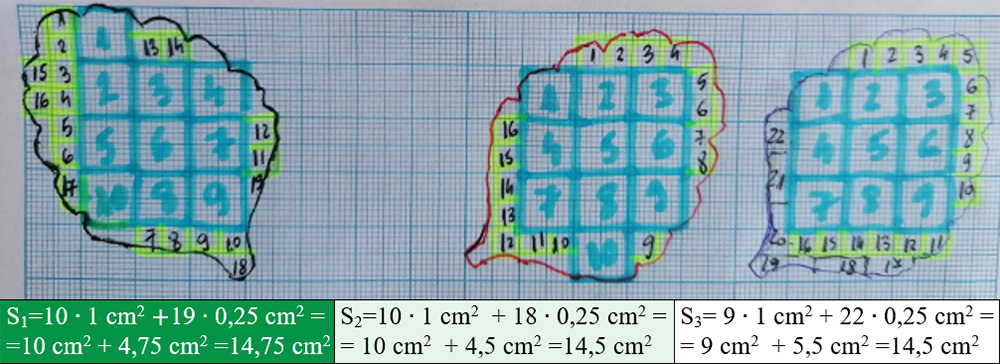
Fill in the experimental data table and process the data in the table.

Experiment conclusion:
So the real area of the leaf is: S = S_average ± ΔS_average = 14,58 cm² ± 0,11cm².

🔓 Solved problems - Indirect determination of the area

2.4. A tennis court (rectangular) has a length of 2,377 dam and a width of 8230 mm for single play. Calculate the area of the rectangle in m².

Solution:

We note the data of the problem and transform the given parameters into SI:

We apply the formula for calculating the area of a rectangle and replace the problem data. Always add the measurement unit to the obtained result.

S = L ∙ l = 23,77 m ∙ 8,23 m = 195,62 m²

2.5. A certain triangle has a side of 0,008 km and the height corresponding to this side is 670 cm. Find the area of the surface of this triangle.

Solution:

We note the data of the problem and transform the given parameters into SI:

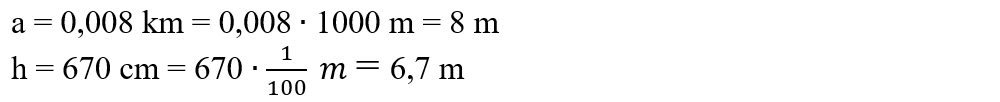
We apply the formula for calculating the area of a triangle and replace the problem data. Always add to the result obtained the measurement unit m².

2.6. The floor of a room is covered with square tiles, measuring 40 cm. If you count 10 tiles on the length of the room and 8 tiles on the width, what is the area of the floor surface?

Solution:

We note the data of the problem and transform the given parameters into SI:

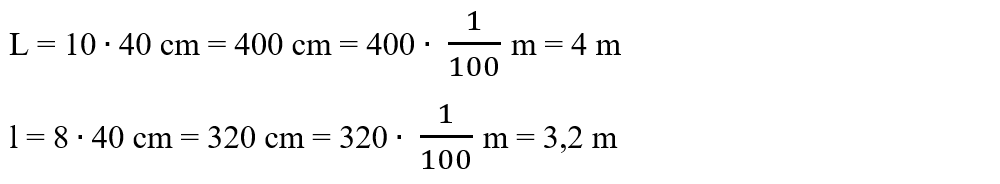
We apply the formula for calculating the area of a rectangle and replace the problem data. Always add the measurement unit to the obtained result.

S = L ∙ l = 4 m ∙ 3,2 m = 12,8 m²

2.7. Calculate the surface areas of a box that has the following dimensions:

L = 22,5 cm

l = 11,3 cm

h = 7 cm

Solution:

We transform the given parameters into SI:

A box (parallelepiped) has six surfaces, two by two equal. So we calculate the areas of rectangular surfaces that are different, that is, three areas. We apply the formula for calculating the area of a rectangle and replace the problem data. The unit of measure is always added to the obtained result.

S₁ = L ∙ l = 0,225m ∙ 0,113 m = 0,025425 m²

S₂ = L ∙ h = 0,225m ∙ 0,07 m = 0,01575 m²

S₃ = l ∙ h = 0,113m ∙ 0,07 m = 0,00791 m²

🔓 Experimental problem - Direct measurement of the volume

2.8. Measuring the volume of a body with the graduated cylinder

Required materials:
Graduated cylinder, water, string, a body.

Experiment description:

2.8.A. The first step is to determine the volume of a division = 1 div = the minimum volume between two consecutive lines. Look carefully at the measurement and find the measurement unit of the cylinder used. How do we proceed?

Note two consecutive graduations (one after the other) of the cylinder and subtract them: 50 ml - 40 ml = 10 ml
Count how many divisions there are between these notations: 10 divisions = 10 ml
With the simple rule of three, we find out the volume of one division:

2.8.B. Put water in the cylinder and measure its volume, denoted by V₁ = 35 ml.

2.8.C. Insert the body into the water in the cylinder. The fluid level has risen. We will note the new volume read V₂ = 39 ml.

2.8.D.. The volume of the body is the difference between V₂ (water+body volume) and V₁ (water volume), ie:

V_body = V₂ – V₁

Remark:

The graduated cylinder must be on a horizontal surface (on the table). The free surface of the liquid is slightly curved (called the meniscus) - higher at the contact of the liquid with the walls of the graduated cylinder. Position the eyes at the free surface of the liquid and read the volume at its base.

Experiment conclusion:

The volume of the body is the difference between V₂ (water volume + body) and V₁ (water volume), ie:

V_body = V₂ – V₁

V_body = 39 ml – 35 ml = 4 ml.

🔓 Solved problems - Indirect measurement of the volume

2.9. A room has a length of 0.06 hm, a width of 40 dm and a height of 330 cm. Calculate the volume of air in the room in m³.

Solution:

We note the data of the problem and transform the given parameters into SI:

The air being a gas occupies the entire volume of the room. We apply the formula for calculating the volume of a parallelepiped and replace the problem data. Always add the measurement unit to the obtained result.

V = L ∙ l ∙ h = 6 m ∙ 4 m ∙ 3,3 m = 79,2 m³.

2.10. Pour 500 cm³ of water into a coffee maker to make the coffee. Knowing that a cup of coffee has 150 mL, how many coffees have you made?

Solution:

We note the data of the problem and transform the given parameters into SI:

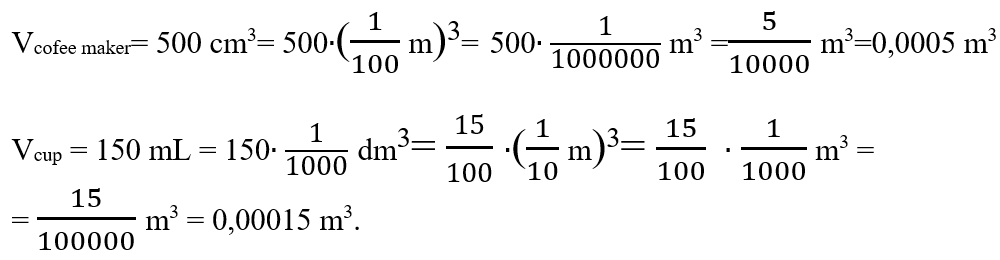
We divide the volume of the coffee maker by the volume of the cup:

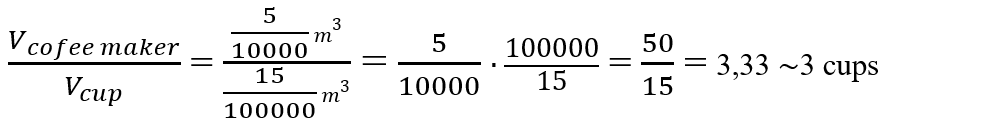
2.11. Determine the volume of the body in the following image, knowing that only water is placed in the first cylinder, and in the second was added to the water from the first cylinder, the body whose volume you need to determine.

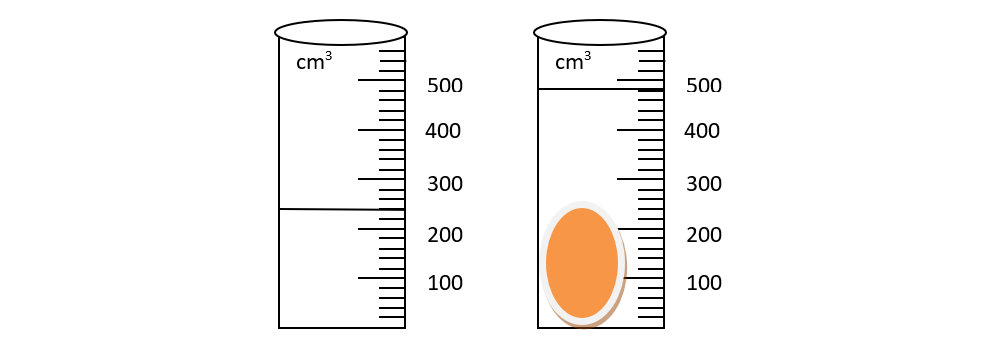
Solution:

🔓 Experimental problem - Direct measurement of the time interval

2.12. Measuring the period of a pendulum with a stopwatch

Required materials:
Ball or nut, thread, stopwatch (you can use the phone)

Experiment description:

Take a small and heavy body (a ball, a nut, a key, etc.) and tie it to the end of a wire to get a pendulum. Attach the wire to a horizontal support (for example, a table).
Remove the wire from the (vertical) equilibrium position and lift it to one side. Then release it and the pendulum will move to either side of this position, ie it will start to oscillate. The stopwatch starts when the body is released.
Measure the time interval (t) in which the body returns a number of times "n" to point A ("n" can have different values: 3, 5, 8, 10 etc. - as much as you want).
Repeat the operation at least 3 times, giving it to "n" different values.
Calculate the period (T) = the time in which the body makes a complete oscillation, ie the time in which the pendulum climbed to the other side and returned to the initial position (round trip). If in a time "t" are performed "n" full oscillations, then the period (T) is calculated using the relation:

Fill in an experimental data table using the below template.

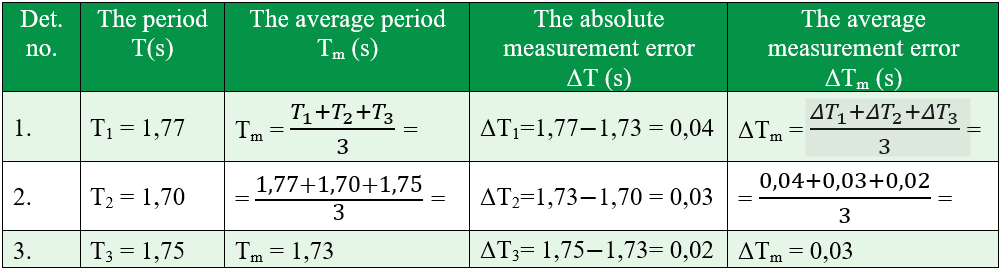
Experiment conclusion:
Write the measurement result: T = T_mean ± ΔT_mean = 1,73 ± 0,03 (s)

🔓 Solved problem - Direct measurement of the time interval

2.13. A movie broadcast on a TV station started at 20:30 and ended at 22:20. If he was interrupted by four commercials, each lasting 8 minutes, how long did the film last, expressed in hours, minutes and seconds?

Solution:

We calculate the broadcast time of both the film and the advertisement, subtracting the end time from the start time of the film: to decrease the minutes, I borrow from the unit of hours by one hour, ie 60 minutes and add them to 20 minutes and say 80 min - 30 min = 50 min.
Then decrease 21 h - 20 h = 1h. 22:20 - 20:30 = 1 h 50 min = t₁.

We calculate the time of the advertising blocks (sequences): t₂ = 4 ∙ 8 min = 32 min

To find out the length of the movie only, subtract t₂ from t₁:

t_movie = t₁ – t₂ = 1 h 50 min – 32 min = 1 h 18 min
t_movie = 60 min + 18 min = 78 min = 78 ∙ 60 s = 4680 s

To find out the duration in hours we transform 18 min into h with the simple rule of 3: