Cap.IV. Echilibrul corpurilor.

• Probleme rezolvate.
• Exerciții recapitulative.
• Test de autoevaluare.

Probleme rezolvate.

🔓 Problemă rezolvată - Echilibrul de translație.

4.1. Determină dacă următoarele corpuri sunt în echilibru de translaţie:

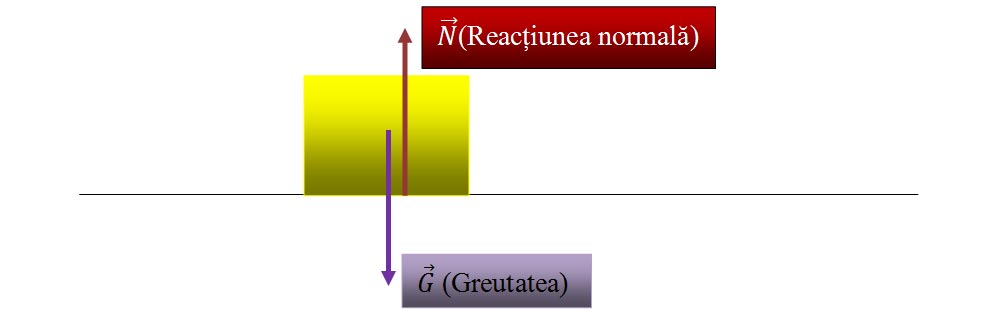
4.1.A. Un corp sprijinit pe o suprafață (podea, masă, scaun etc.) în stare de repaus.

Rezolvare:

În stare de repaus, un corp sprijinit pe o suprafață (podea, masă, scaun etc.) are forța rezultantă egală cu zero, deoarece avem modulul greutății egal cu modulul reacțiunii normale:
| G | = | N |.

Forța rezultantă este:
R = N – G = 0 deci corpul este în echilibru de translație.

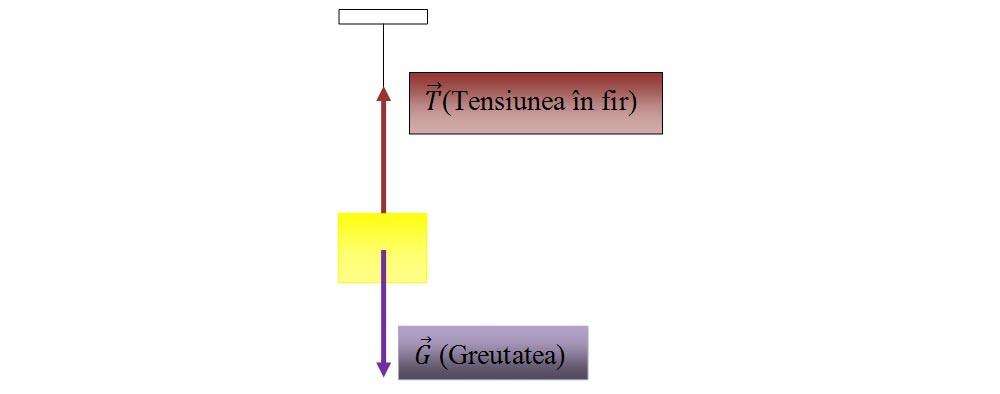
4.1.B. Un corp în repaus suspendat de un fir inextensibil.

Rezolvare:

Un corp suspendat are forța rezultantă egală cu zero, deoarece avem modulul greutății egal cu modulul tensiunii în fir:
| G | = | T |.

Forța rezultantă este:
R = T – G = 0 deci corpul este în echilibru de translație.

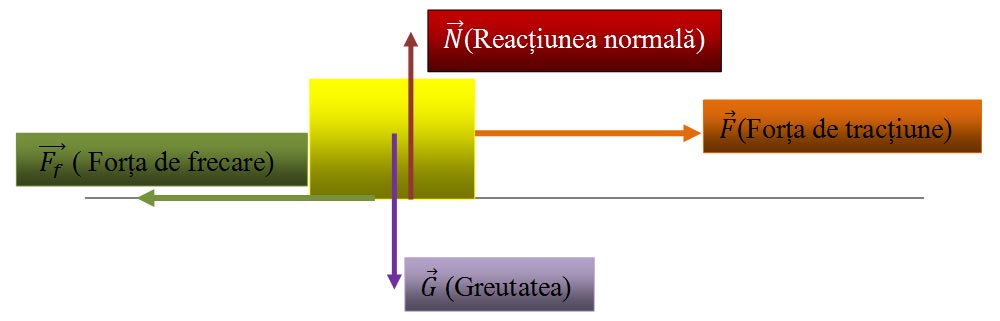
4.1.C. Un corp în stare de mişcare rectilinie uniformă.

Rezolvare:

Un corp în stare de mişcare rectilinie uniformă are forța rezultantă egală cu zero.
Pe direcția orizontală ( O_x ) : | F | =| F_f | => R_x = F – F_f = 0
Pe direcția verticală ( O_y ) : | G | = | N | => R_y = N – G = 0

Corpul este în echilibru de translație.

🔓 Probleme rezolvate - Echilibrul de rotație

4.2. O forță de 40 N acționează pe direcția axei de rotație a unui disc. Rotește această forță discul?

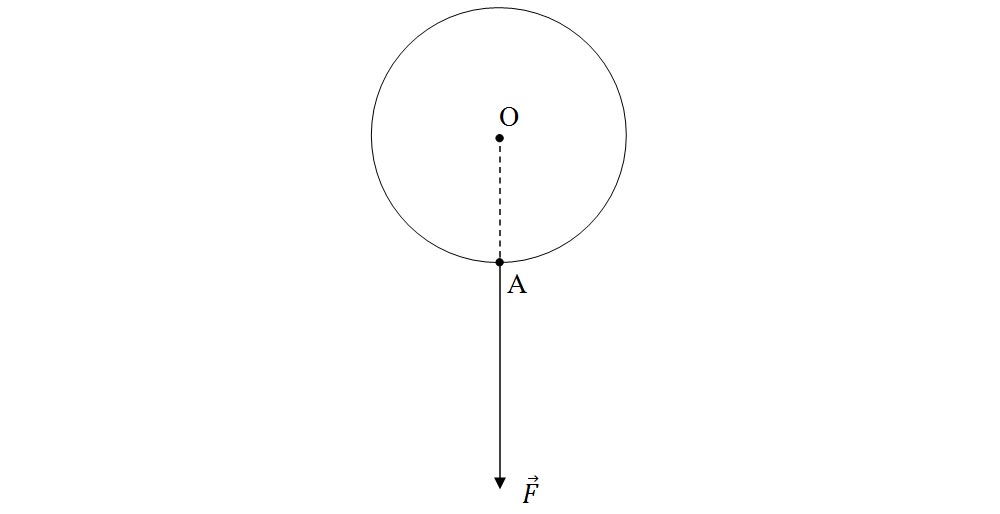
Rezolvare:

Deoarece b_F = 0, atunci și M_F = 0 ( momentul forței este zero) și forța aplicată nu rotește discul.

4.3. O forță de 40 N acționează pe verticală, în jos, la marginea din dreapta a unui disc. Rotește această forță discul? Se dă raza discului de 6 cm.

Rezolvare:

Ducem perpendiculară din centrul cercului (O) pe direcția forței și așa aflăm brațul forței, care este egal cu raza discului.

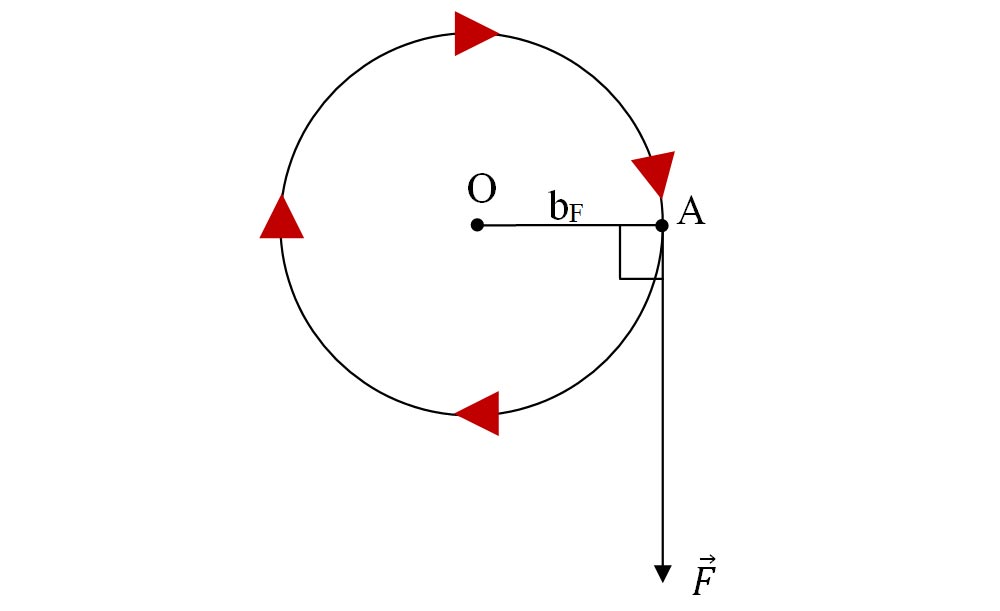
Calculăm momentul forței:

4.4. Asupra unui disc cu raza de 20 cm acționează trei forțe ca în figura de mai jos:

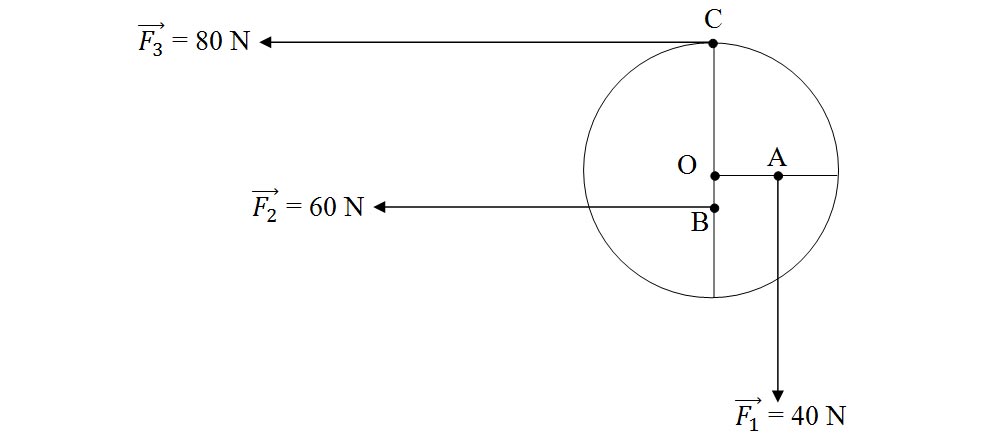
Rezolvare:

Se stabilește sensul fiecărei forțe ca și cum ar acționa singură asupra discului:
Sens orar: F₁, F₂
Sens antiorar: F₃.

Se calculează brațele fiecărei forțe și se transformă în metri:

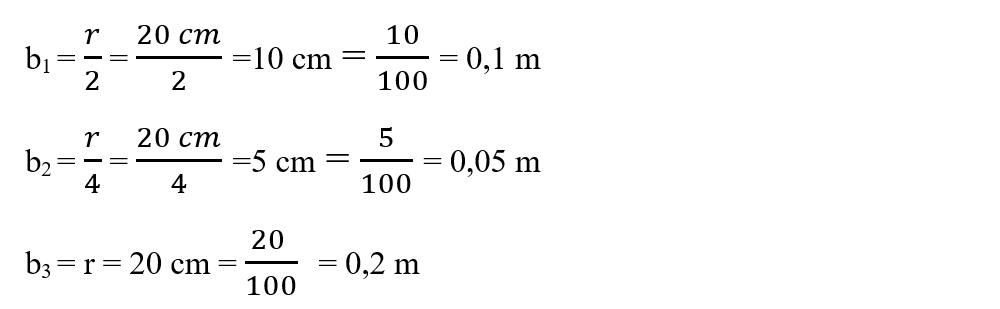
Se calculează momentul orar prin adunarea momentelor forțelor ce ar roti discul în sens orar:
M_orar = M₁ + M₂ = F₁ • b₁ + F₂ • b₂ = 40 N • 0,1 m + 60 N • 0,05 m = 7 N∙m

Se calculează momentul antiorar prin adunarea momentelor forțelor ce ar roti discul în sens antiorar:
M_antiorar = M₃ = F₃ • b₃ = 80 N • 0,2 m = 16 N∙m

Se compară cele două momente:
M_antiorar > M_orar => Discul se rotește în sens antiorar.

🔓 Problemă rezolvată - Pârghia – un mecanism simplu

4.5. Tăiem un cui cu ajutorul unui clește. Distanța nit (articulația cleștelui) la cui este de 3 cm și de la nit la mâner este 5 dm. Mâna strânge cleștele cu 600 N. Cât este forța rezistentă din partea cuiului?

Rezolvare:

Desenăm forțele ce apar la tăierea cu cleștele:

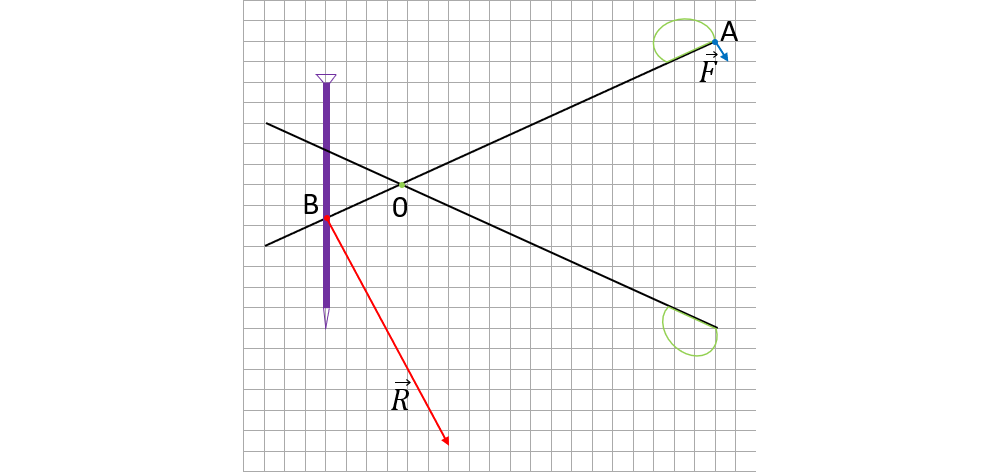
Scriem datele problemei și transformăm în SI:
OB = b_R = 3 cm = 0,03 m
OA = b_F = 5 dm = 0,5 m
F = 600 N
R = ?

Scriem legea pârghiei și scoatem necunoscuta:

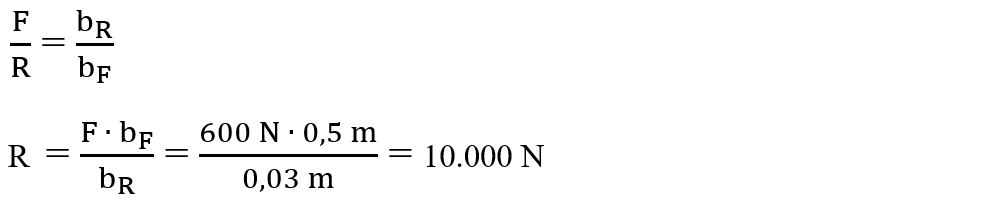
🔓 Probleme recapitulative rezolvate - Echilibrul corpurilor

4.6 Un corp cu greutatea de 300 N se mișcă uniform pe o suprafață orizontală sub acțiunea a două forțe: F₁ = 100 N care face un unghi α₁ = 60° cu orizontala și F₂ = 200 N care face un unghi α₂ = 30° cu orizontala.

a) Să se reprezinte forțele ce acționează asupra corpului.

b) Sensul mișcării corpului.

c) Ce valoare trebuie să aibă forța de frecare și reacțiunea normală ca acest corp să fie în echilibru de translație ?

Rezolvare:

a) Pentru a afla sensul mișcării se compară componentele forțelor de tracțiune pe axa de mișcare, Ox.

F_x1 = F₁ ∙ cos α₁ = F₁ ∙ cos 60° = 100 N ∙ 0,5 = 50 N

F_x2 = F₂ ∙ cos α₂ = F₂ ∙ cos 30° = 200 N ∙ 0,86 = 172 N

Deoarece F_x2 > F_x1, înseamnă că mișcarea corpului se face în sensul forței F_x2, adică spre stânga.

b)

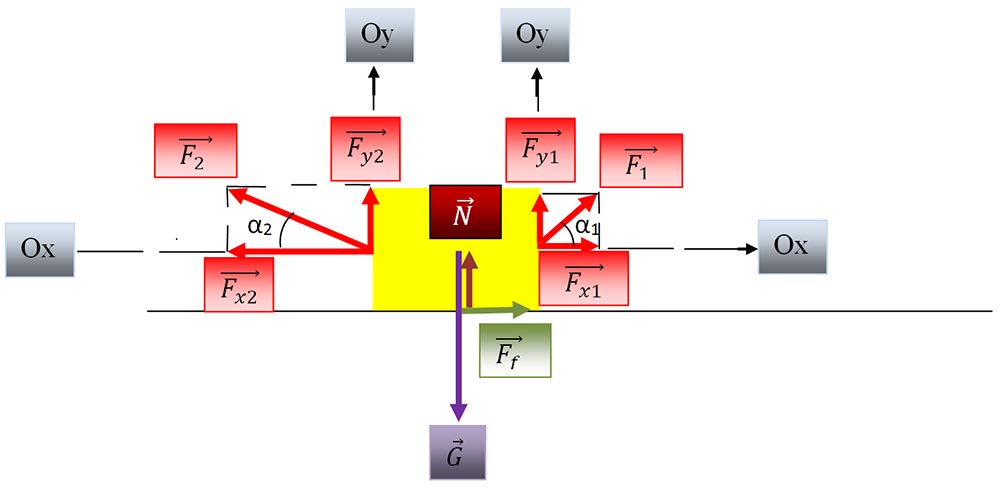
c) Un corp este în echilibru de translație atunci când forța rezultantă ce acționează asupra lui este egală cu zero.

Pe axa Ox punem condiția ca forța rezultantă să fie 0.
| F_x1 + F_f | = | F_x2 |
| 50 N + F_f | = 172 N
F_f = 122 N

Pe axa Oy punem condiția ca forța rezultantă să fie 0. Atunci vom avea următoarea egalitate :
| F_y1 + N + F_y2 | = | G |
F_y1 = F₁ ∙ sin α1 = F₁ ∙ sin 60° = 100 N ∙ 0,86 = 86 N
F_y2 = F₂ ∙ sin α2 = F₂ ∙ sin 30° = 200 N ∙ 0,5 = 100 N
| 86 N + N + 100 N | = 300 N
N = 114 N

4.7. În sens orar acționează asupra unui disc trei forțe:

• F₁ = 50 N, b₁ = 40 cm

• F₂ = 75 N, b₂ = 20 cm

• F₃ = 100 N, b₃ = 10 cm.

În ce sens și ce valoare trebuie să acționeze o a patra forță cu brațul de 50 cm, pentru ca discul să fie în echilibru de rotație?

Rezolvare:

Transformăm brațele celor patru forțe în SI:
b₁ = 40 cm = 0,4 m
b₂ = 20 cm = 0,2 m
b₃ = 10 cm = 0,1 m
b₄ = 50 cm = 0,5 m

Calculăm momentul orar:
M_orar = M_F1 + M_F2 + M_F3 = F₁ ∙ b₁ + F₂ ∙ b₂ + F₃ ∙ b₃ = 50 N ∙ 0,4 m + 75 N ∙ 0,2 m + 100 N ∙ 0,1 m = 20 N ∙ m + 15 N ∙ m + 10 N ∙ m = 45 N ∙ m

Calculăm momentul antiorar:
M_antiorar = M_F4 = F₄ ∙ b₄ = F₄ ∙ 0,5

Scriem condiția echilibrului de rotație:
M_orar = M_antiorar
45 = F₄ ∙ 0,5
F₄ = 45/0,5 = 90 N

4.8 Valentin a realizat un montaj format dintr-un scripete fix și trei scripeți mobili.

a) Desenează montajul realizat de Valentin.

b) Cu ce forță trebuie să tragă Valentin asupra firului acestui montaj de scripete compus pentru a ridica uniform un corp de 16 kg ?

c) Cât este distanța pe care se deplasează punctul de aplicație al forței lui Valentin, știind înălțimea la care a ridicat corpul este de 0,6 m.

Rezolvare:

a)

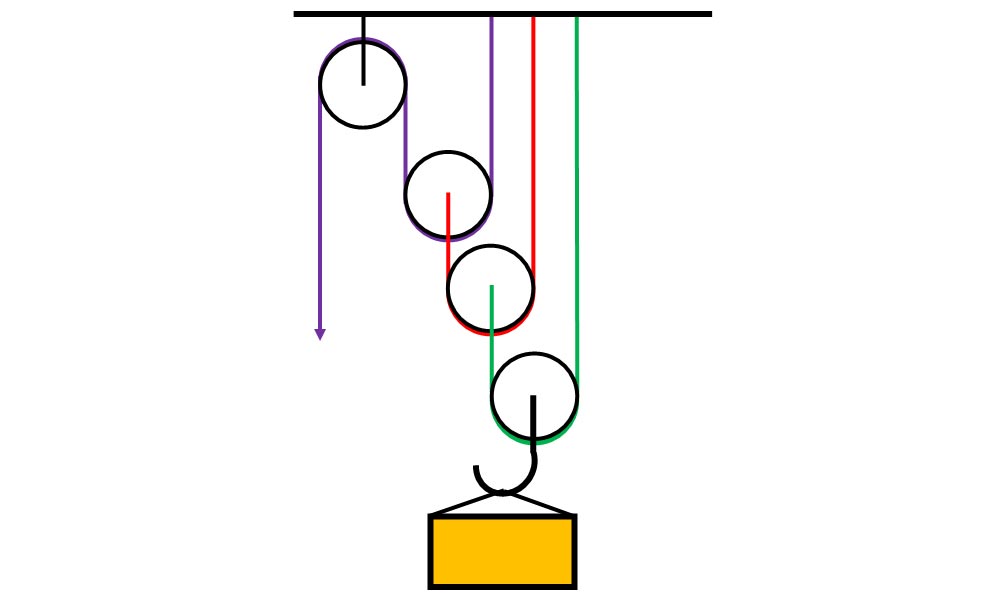
b) m = 16 kg

R = G = m ∙ g = 16 ∙ 10 = 160 N

Pentru n = nr. de scripeți mobili, avem formula care ne dă legătura între forța activă (F) și forța rezistentă (R):

c) Pentru n = nr. de scripeți mobili, avem formula care ne dă legătura între distanța parcursă de punctul de aplicație al forței active (dF) și distanța parcursă de punctul de aplicație al forței rezistente (d_R = h = înălțimea la care este urcat corpul) :

d_F = 2ⁿ ∙ h = 2³ ∙ 0,6 = 4,8 m

4.9. Dintr-un disc circular omogen cu raza R = 10 cm se taie un disc cu raza r = 5 cm, tangent interior la discul mare. Să se determine poziția centrului de greutate al porțiunii rămase.

Rezolvare:

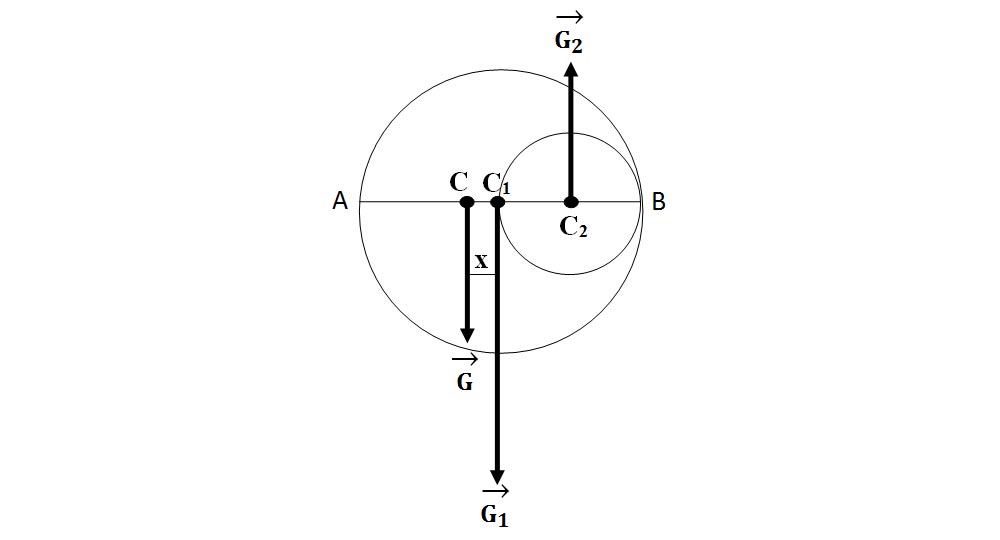
La un cerc centrul de greutate este chiar în centrul cercului, adică la o distanță egală cu raza cercului față de marginea acestuia.

Discul mare are centrul de greutate în C₁, la care R = C₁A = 10 cm.
Discul mic are centrul de greutate în C₂, la care r = C₂B = 5 cm.
Porțiunea decupată va avea centrul de greutate în C, la distanța x față de C₁ și va reprezenta punctul de aplicație al greutății G, care este rezultanta forțelor G₁ și G₂.
Deoarece porțiunea circulară este decupată, ea va avea greutatea G₂ opusă greutății G₁ (va trebui scăzută din greutatea totală, G₁).

Punem condiția echilibrului de rotație astfel încât momentul forței G₁ față de C să fie egal cu momentul forței G₂ față de C.

Notăm cu d = grosimea plăcii pentru a putea calcula greutatea celor două discuri:

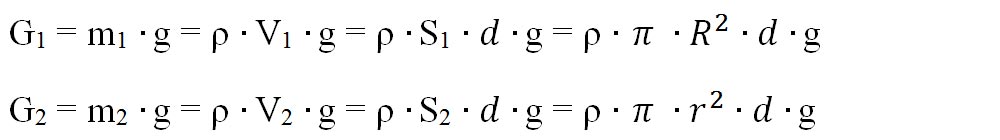
Înlocuim aceste valori în condiția de echilibru de rotație:

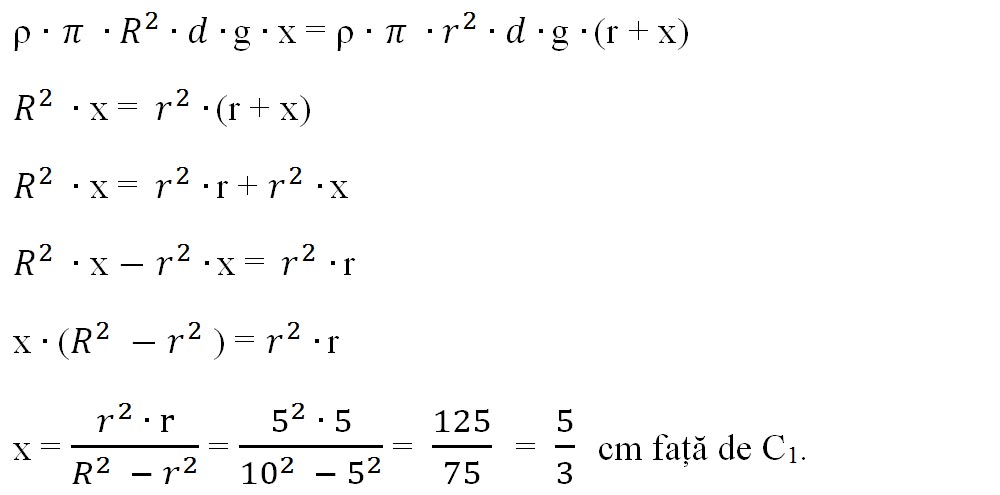
4.10. Dintr-o placă pătrată omogenă și de grosime, d, constantă, având latura de l₁ = 24 cm se taie un pătrat cu latura l₂ = 12 cm. Să se determine poziția centrului de greutate al porțiunii rămase.

Rezolvare:

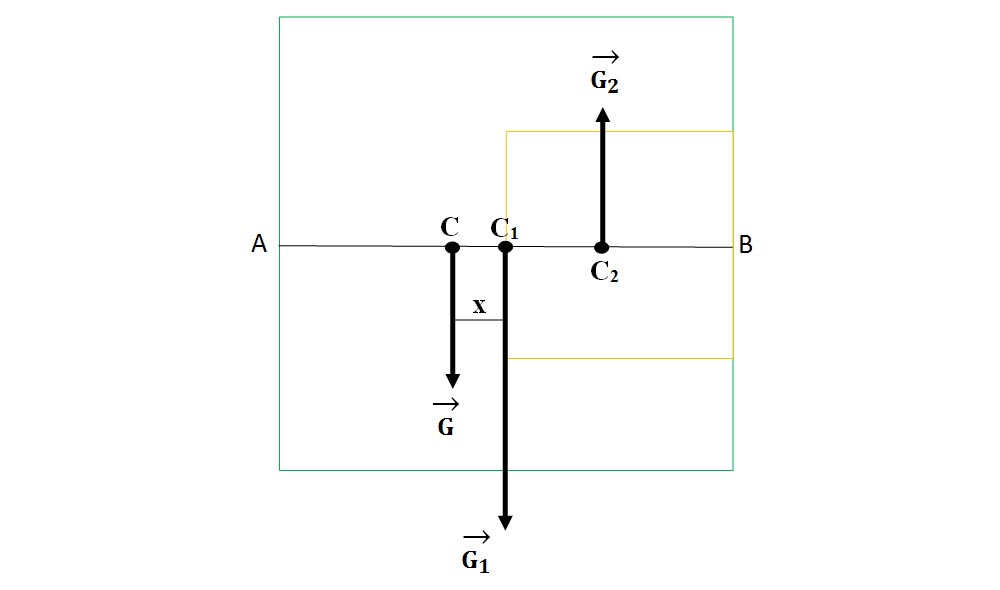
La un pătrat centrul de greutate este în intersecția diagonalelor, adică la o distanță egală cu jumătate din latura sa față de marginea acestuia.

Pătratul mare are centrul de greutate în C₁, la care C₁A = 12 cm.
Pătratul mic are centrul de greutate în C₂, la care C₂B = 6 cm.
Porțiunea decupată va avea centrul de greutate în C, la distanța x față de C₁ și va reprezenta punctul de aplicație al greutății G, care este rezultanta forțelor G₁ și G₂.
Deoarece pătratul mic este decupat, el va avea greutatea G₂ opusă greutății G₁ (va trebui scăzută din greutatea totală, G₁).

Punem condiția echilibrului de rotație astfel încât momentul forței G₁ față de C să fie egal cu momentul forței G₂ față de C.

Notăm cu d = grosimea plăcii pentru a putea calcula greutatea celor două discuri:

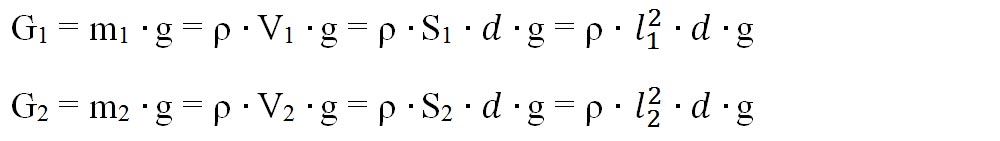
Înlocuim aceste valori în condiția de echilibru de rotație:

4.11. Șurubul este și el un mecanism simplu, din categoria planului înclinat. Este format dintr-un cilindru pe care este săpat un șanț elicoidal, având în partea superioară un tambur prevăzut pe mijloc cu un șanț și care poate fi rotit cu ajutorul unei șurubelnițe sau a unei chei. Pasul șurubului se notează cu h și reprezintă distanța pe care înaintează șurubul în piuliță într-o rotație completă.

Ce apăsare realizează un șurub cu pasul de 1 mm, dacă rotim capul șurubului, cu o cheie ce are un braț b=40cm și acționăm cu o forță de 5 N ?

Rezolvare:

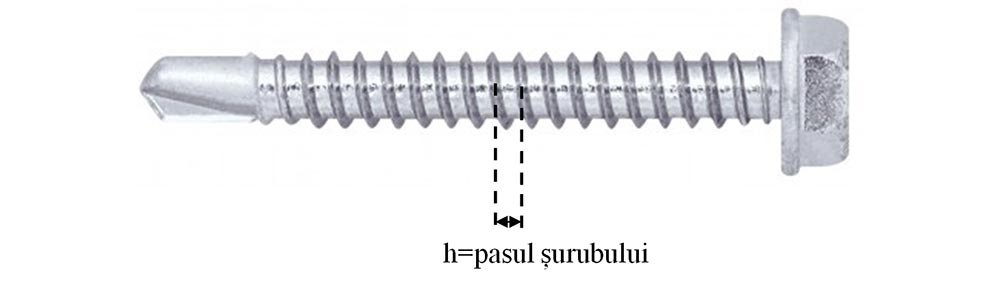
Scriem datele problemei și le transformăm în SI:
h = 1 mm = 0,001 m
b = 40 cm = 0,4 m
F = 25 N
R = ?

La o rotație completă a șurubului, omul va efectua un lucru mecanic:
L_F = 2 ∙ π ∙ b

Lucrul mecanic al forței rezistente la înaintarea șurubului cu pasul h este:
L_R = R ∙ h

Aplicăm principiul conservării lucrului mecanic (F_f = 0):

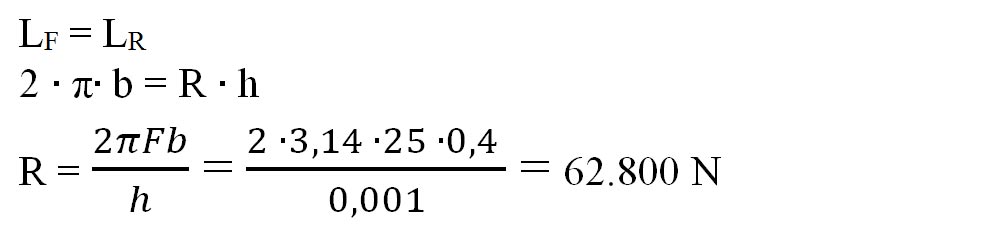
Apăsarea exercitată de șurub este direct proporțională cu forța exercitată de om asupra cheii și cu brațul cheii.

Apăsarea exercitată de șurub este invers proporțională cu pasul șurubului. Deci, un șurub cu pasul mai mic stânge mai bine decât unul cu pasul mai mare.

4.12. Bara AB este în echilibru. Corpurile ce echilibrează bara au masele m₁ = 15 kg, respectiv m₂ = 30 kg. Determină masa barei AB.

Rezolvare:

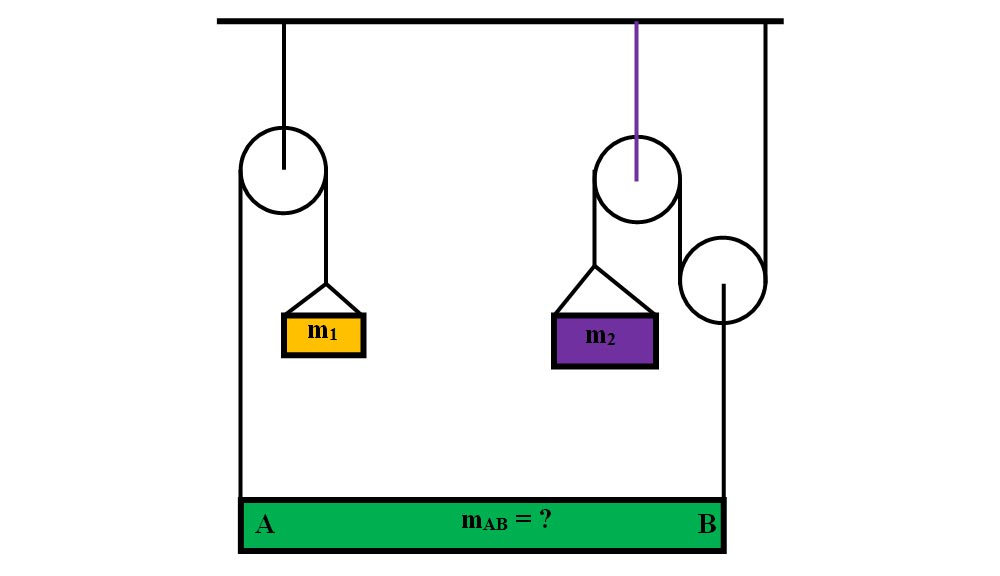
Scriem datele problemei:
m₁ = 15 kg
m₂ = 30 kg
m_AB = ?

Calculăm forțele ce acționează asupra capetelor barei, F₁ și F₂.

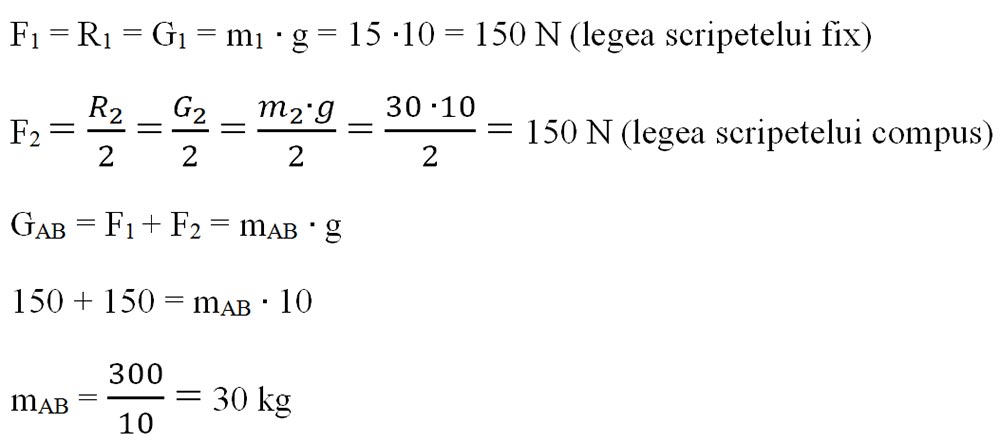
4.13. Vlad dorește să ridice un corp cu greutatea de 800 N cu o rangă având lungimea de 1,8 m. El acționează asupra barei cu o forță de 100 N. Unde trebuie Vlad să așeze punctul de sprijin al acestei pârghii?

Rezolvare:

Scriem datele problemei:
R = G = 800 N
AB = OA + OB = b_F + b_R = 1,8 m
F = 100 N
OB = ?

Scriem legea pârghiei și înlocuim datele problemei:

4.14. Asupra unei plăci sub forma unui pătrat cu latura de 20 cm, ce se poate roti în jurul punctului O, acționează patru forțe egale cu modulul de 40 N, ca în figura de mai jos:

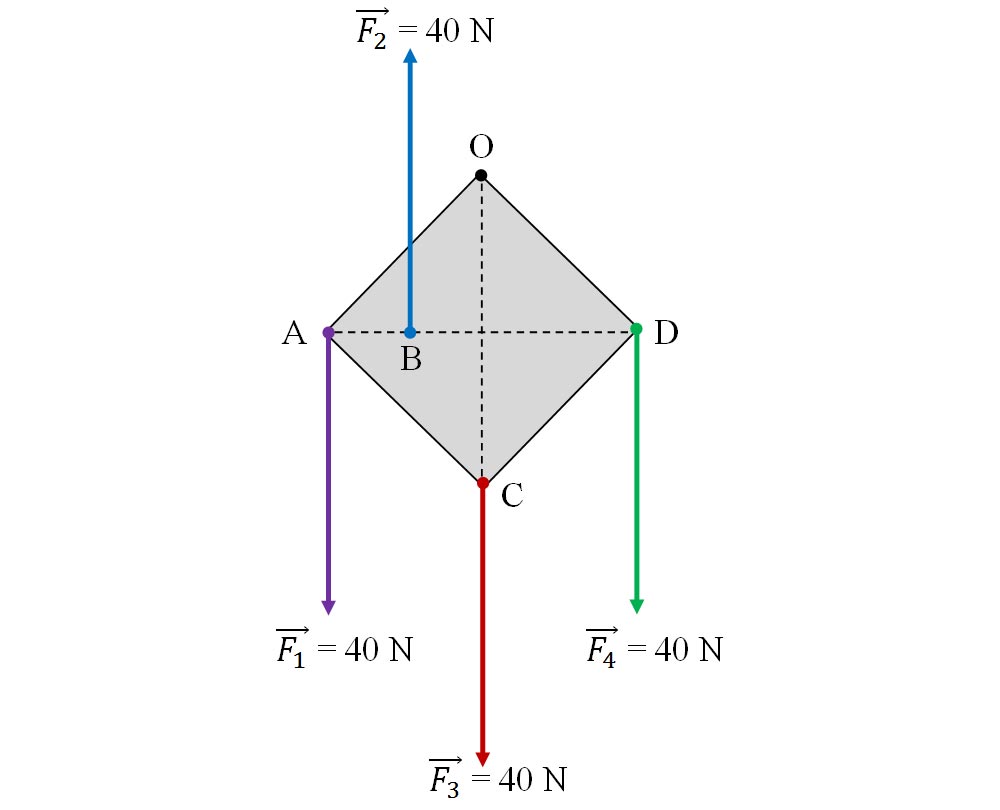
Datele problemei:
F₁ = F₂ = F₃ = F₄ = 40 N
AO = OD = CD = AC = l = 20 cm

Determină:

a) Care forță nu produce rotația plăcii?

b) Care dintre forțe formează un cuplu de forțe? Calculează momentul cuplului.

c) Determină dacă placa este în echilibru de rotație.

Rezolvare:

a) Forța F₃ nu produce rotația plăcii, deoarece dreapta ei trece prin axa de rotație și are brațul zero (nu putem duce nicio perpendiculară de la O la dreapta forței). Având brațul nul și momentul ei va fi nul.

b) Cuplu de forțe este format din forțele F₂ și F₄, deoarece ele sunt egale în modul, paralele și au sensuri opuse.

Pentru a afla b₂ ducem perpendiculară din O pe dreapta forței F₂ și vedem că este un sfert din diagonala pătratului (AD/4).
AD = l • √2 = 20 • √2 cm = 20 • √2/100 m
b₂ = AD/4 = 0,05 • √2 m = 0,05 ∙ 1,41 = 0,07 m

Pentru a afla b₄ ducem perpendiculară din O pe dreapta forței F₄ și vedem că este jumătate din diagonala pătratului (AD/2).
b₄ = AD/2 = 0,1 • √2 m = 0,1 ∙ 1,41 = 0,14 m
M_c = M_F2 + M_F4 = F₂ • b₂ + F₄ • b₄ = 40 N • 0,07 m + 40 N • 0,14 m = 2,8 N ∙ m + 5,6 N ∙ m
M_c = 8,4 N ∙ m

Acest cuplu ar roti placa în sens orar (dacă ar fi singur).

c) Pentru a vedea dacă placa este în echilibru de rotație sau nu, trebuie să calculăm momentul forței F₁, care rotește placa în sens antiorar (dacă ar fi singură).

Pentru a afla b₁ ducem perpendiculară din O pe dreapta forței F₁ și vedem că este jumătate din diagonala pătratului (AD/2).
b₁ = AD/2 = 0,1 • √2 m = 0,1 ∙ 1,41 = 0,14 m
M_antiorar = M_F1 = F₁ • b₁ = 40 N • 0,14 m = 5,6 N ∙ m
M_orar = M_c = 8,4 N ∙ m

Se compară cele două momente:
M_orar > M_antiorar => Discul se rotește în sens orar și nu este în echilibru de rotație.

Exerciții recapitulative.

🔐 Exerciții recapitulative - Echilibrul corpurilor

4.15. Completează următoarele afirmații:

a) Un corp solid are o mişcare de translaţie dacă oricare ar fi două puncte ale corpului, segmentul ce le uneşte îşi păstrează ………………… în timpul mişcării.

b) Un corp solid are o mişcare de ……………… în jurul unei axe atunci când traiectoria corpului este un arc de cerc cu centrul în axul de rotaţie.

c) Un corp este în ……………………………………………………… atunci când rezultanta tuturor forțelor ce acționează asupra lui este zero.

d) Un corp este în echilibru de rotaţie atunci când suma momentelor forțelor ce rotesc corpul în sens ………… este egală cu suma momentelor forțelor ce rotesc corpul în sens …………...

e) Pârghia este o …………… rigidă ce se poate …………în jurul unui punct de sprijin (O), asupra căreia acționează două forțe:

• f) forța ………………… , forța cu care omul acționează asupra pârghiei

• g) forța …………………, forța ce trebuie învinsă cu ajutorul pârghiei.

h) Centrul de greutate este punctul de aplicație al ……………………… unui corp.

i) Corpurile suspendate sunt în echilibru stabil când centrul de greutate este ……………… punctul de suspendare, pe aceeași ………….

j) Corpurile sprijinite sunt în echilibru stabil când verticala dusă din centrul de greutate cade …………………. bazei de sprijin.

k) Corpurile suspendate sunt în echilibru instabil când centrul de greutate este ………… punctului de susținere, pe aceeași ………….

l) Corpurile sprijinite sunt în echilibru instabil când verticală dusă din centrul de greutate (C ) cade pe ……………. bazei de sprijin.

m) Corpurile suspendate se află în echilibru indiferent când punctul de susținere este în …………………………………………… .

n) Corpurile sprijinite se află în echilibru indiferent când sunt pe o suprafață ………………. și la mari deviații rămân tot în echilibru.

4.16. Scrie în dreptul fiecărui exemplu ce fel de mișcare are corpul menționat:

• Sertarul față de șine

• Deschiderea și închiderea ușilor și ferestrelor față de balamale.

• Ușile glisante față de șine

• Mișcarea telecabinei (telegondolei, telescaunului) față de cablu

• Înșurubarea unui șurub cu șurubelnița

• Mișcarea unui robinet

• Căderea liberă a corpurilor

• Mișcarea grătarului unui cuptor de aragaz

4.17. Precizează în dreptul fiecărei pârghii de ce ordin este:

• Roaba

• Balanța

• Penseta

• Foarfecele

• Cleștele de scos sâmburi de vișine

• Levierul

• Cleștele de spart nuci

4.18. Desenează, scrie legea și avantajele și dezavantajele scripetelui:

a) Fix

b) Mobil

4.19. Determină centrul de greutate al următoarelor corpuri omogene plane:

a)

b)

c)

4.20. Scrie în dreptul fiecărui corp în ce fel de echilibru este și de ce:

a)

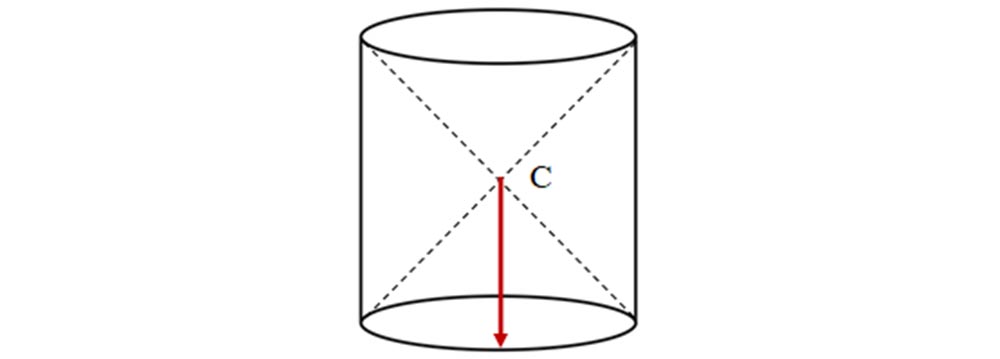
b)

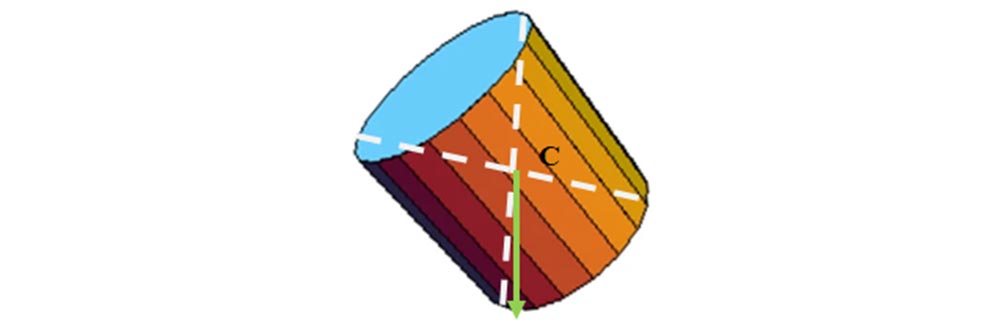
c)

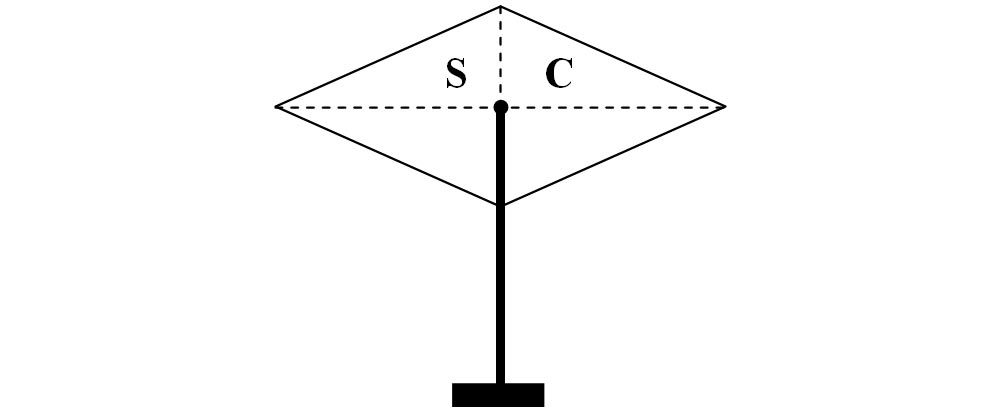
d)

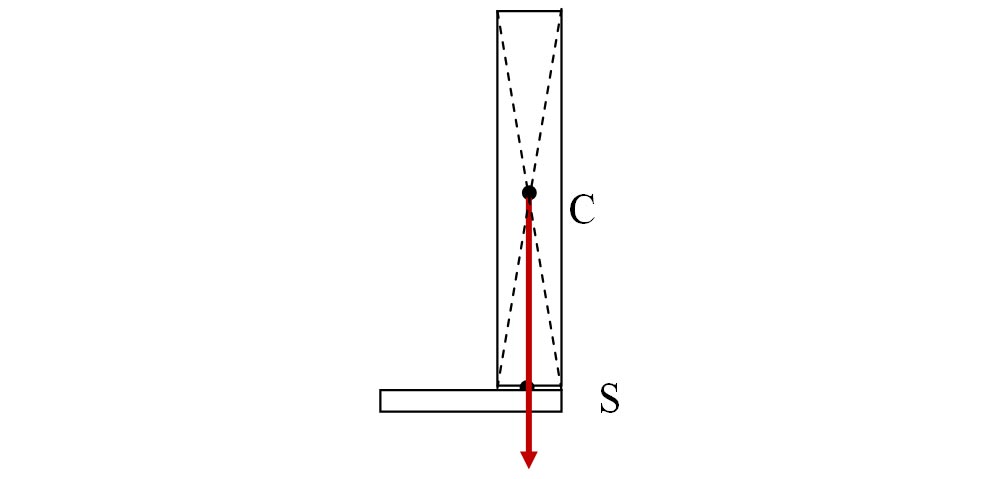
e)

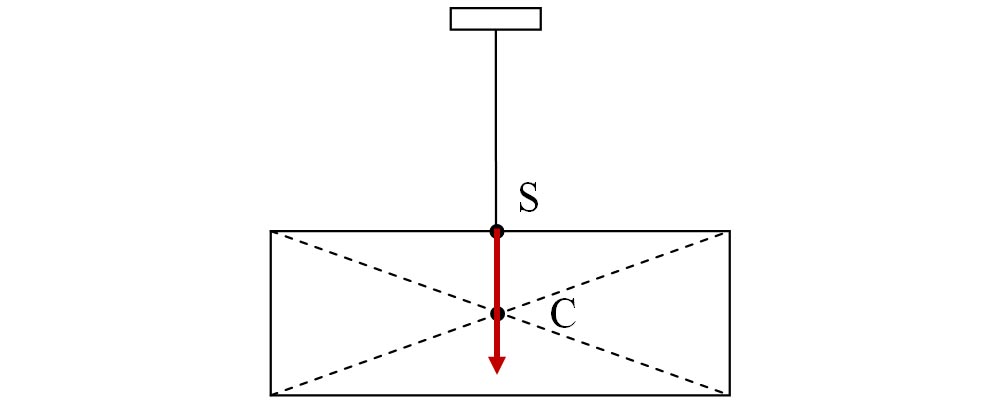
f)

4.21. Demonstrează că un corp aflat în mișcare uniformă tras de o forță de tracțiune pe o suprafață orizontală este în ehilibru de translație.

4.22. Determină dacă următorul disc este în echilibru de rotație. Se dă raza discului de 80 mm.

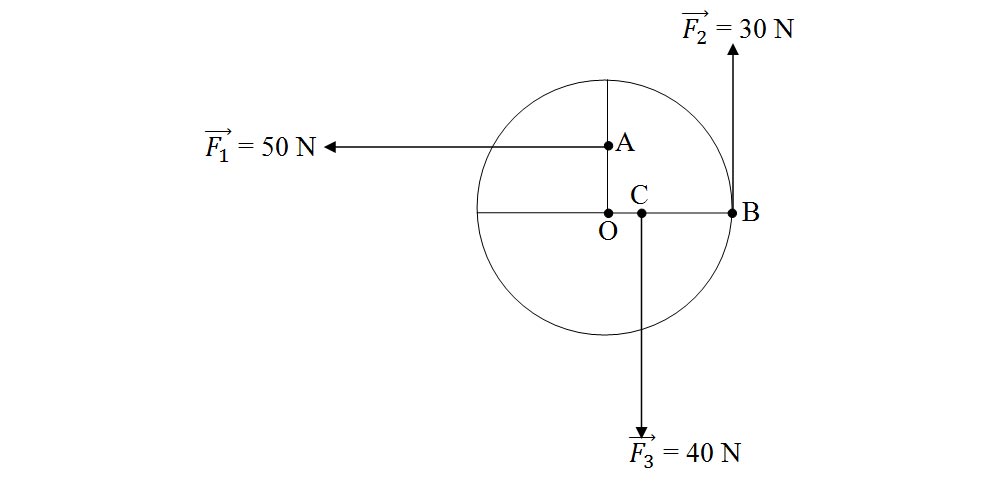
4.23. Matei acționează asupra unei roabe cu o forță de 150 N. Știind că distanța de la axul roții până la mijlocul cutiei este de 30 cm, iar de la mijlocul cutiei până la mâner este de 60 cm, află ce greutate maximă poate ridica Matei cu această roabă?

4.24. Irina a pictat la ora de desen un peisaj pe un carton sub forma unui triunghi echilateral cu latura de 4 cm. Fiind reușit, dorește să îl suspende pe perete. În ce echilibru va fi tabloul Irinei suspendat în unul din cele trei vârfuri?

4.25. Turnul din Pisa (în italiană Torre di Pisa) este cea mai faimoasă clădire înclinată din lume și punctul de reper al orașului Pisa din Italia. În ce fel de echilibru este acest turn?

4.26. Desenează:

a) O pensetă

b) Un patent

c) Un clește de spart nuci.

Test de autoevaluare.

📝 TEST1: Test de autoevaluare - Echilibrul corpurilor

4.27. Precizează ce fel de mișcare au următoarele corpuri: -1p

a) Sertarul față de șine

b) Ușa față de balamale

c) Acul magnetic față de ax

d) Telecabina față de cablu.

4.28. Completează următoarele afirmații: -1p

a) Un corp este în mișcare de rotație dacă traiectoria sa este ………………………

b) Un corp este în mișcare de translație dacă segmentul ce unește oricare două puncte ale corpului……………………………………………………………….

4.29. De ce jucăria Hopa-Mitică nu se răstoarnă și revine tot timpul în poziția inițială? -1p

4.30. Determină în ce fel de echilibru este următorul corp: -1p

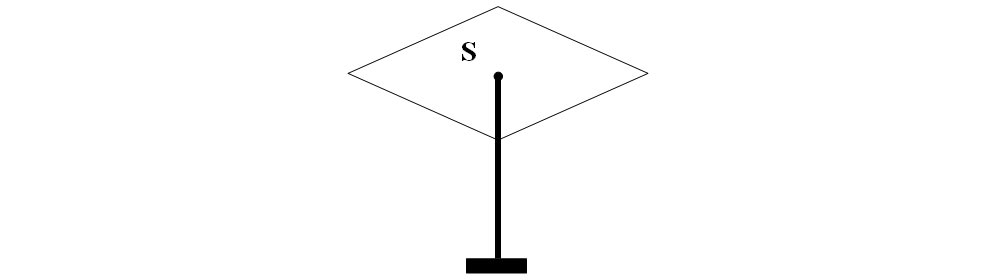
4.31. Desenează un scripete fix, scrie legea sa și precizează un avantaj și un dezavantaj al folosirii acestuia. -1p

4.32. Ionuț taie cu un clește o sârmă, acționând cu o forță de 150 N. Distanța de la sârmă la nit (articulația cleștelui) este de 10 cm. Forța rezistentă din partea sârmei este de 900 N. Cât este distanța de la nit la mânerul cleștelui? -1,5p

4.33. Știind raza discului din imagine este de 4 dm, află dacă acest disc este în echilibru de rotație. -1,5p

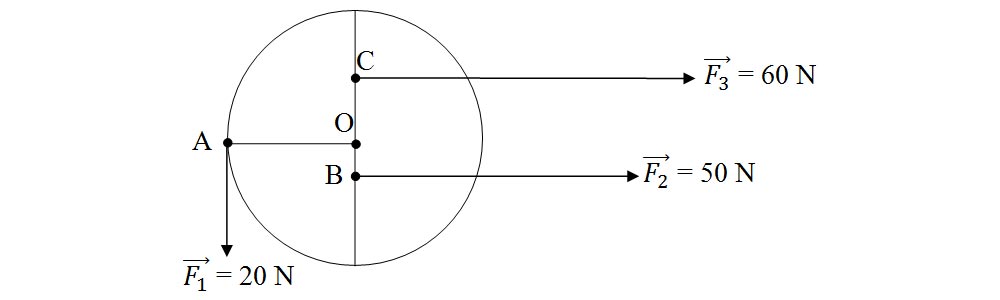
Din oficiu -2p